Polar Alignment Method

Featuring the Collins method of precise polar alignment

This page describes the quickest, most accurate method of polar alignment. It is targeted for those without a permanent setup, where polar alignment must be done at the beginning of each observing session. This page assumes that you have some understanding of telescopes already, and assumes that you can use a calculator and work out equations where necessary.

Polar alignment can be broken down into 3 steps.

Rough polar alignment

Better polar alignment

Precise polar alignment

The steps should be performed in order, stopping when the alignment is suitable for the intended activity of the night. The duration and accuracy of the current step depends on the accuracy of the previous step.

Rough polar alignment

Northern Hemisphere:

Rough polar alignment alone is a very good choice if you are hosting a drunken hoot. Trying to impress the banshee with a galactic cluster? Then rough polar alignment is all you need.

1. Assemble the scope and tripod.

2. Adjust the declination to be at or near 90 deg. Don’t bother the with mount’s setting circles: you will know when the declination is correct when you sweep the right ascension (RA) back and forth and the optical tube assembly (OTA) remains pointed in the same direction, and only rotates around.

Swing RA, fork mounted, Schmidt Cassegrain (SCT) example

Swing RA, German equatorial mount (GEM) example

3. Dial in your latitude into the mount’s altitude adjustment.

4. Adjust the mount’s azimuth adjustment until the OTA is pointed in the general direction of North.

Stop there. That’s it. Seriously, don’t bother going any further. If you spend the time doing the better polar alignment or precise polar alignment, other people will drink your beer and some jerk will steal the banshee you were trying to impress in the first place. At the very most, if you have an extra minute or two, use the polar finder on your mount if it has one, or get Polaris in your finderscope’s field of view by adjusting the altitude and azimuth – just be sure to make it quick. Now the stars are at your fingertips.

Southern Hemisphere:

Perform the procedure described above, except point the OTA in the general direction of the southern pole (declination -90 deg), instead of the northern pole.

Better polar alignment

Northern hemisphere:

So tonight is a relatively sober night. If you have a little more time, you may wish to invest in the time to do a somewhat more precise job of polar alignment.

1. Perform the rough polar alignment as described above, except substitute coffee for beer.

2. Open up the right ascension (RA) locks, and swing the RA back and forth while looking in the eyepiece (you’ll probably want to use your lowest power eyepiece). Look into the eyepiece such that the tip of your head is pointed toward true North. Adjust the declination to bring the center of rotation into the field of view. Keep making adjustments until the center of rotation is center in the field of view in the up/down direction.

Adjusting the declination moves the center of RA rotation in the up/down direction. When the center of rotation is in the field of view, don’t be alarmed if it is not perfectly centered in the left/right direction. It’s not a big deal. If you really wanted to correct for an offset in the left/right direction, you would need to fiddle with attachment mechanism between the OTA and the mount. On many if not most mounts, there is no easy access to this type of adjustment. But again, a little left/right offset is not a big deal. As long as the center of rotation is somewhere within the field of view, you’re good too go.

3. Lock down the declination lock. Orient the RA such that the scope is level – not tilting either East or West, roughly. Lock down the RA lock. The eyepiece should be pointing up toward the celestial equator and the meridian (assuming a diagonal is being used).

4. Using the altitude and azimuth adjustments only (on the mount), center Polaris at the center of RA rotation (see step 2).

You can check to ensure that Polaris is in the center of RA rotation by temporarily unlocking the RA lock, and swinging the RA back and forth. Once finished, recenter the RA and lock down the RA lock.

5. We’d be finished now if Polaris was actually at true North. But it isn’t. True North is about 0.7 degrees away from Polaris, in the general direction of Alkaid – the last star in the Big Dipper’s handle. So we need to make another adjustment. But first, you must calculate the angular distance from the center of your eyepiece to its edge. This distance is ½ the apparent field of view of your eyepiece, divided by the magnification. Look up your eyepiece specs if you don’t know. For example, standard Plössl eyepieces have around 50º apparent field of view (yours may differ slightly). Televue Nagler eyepieces have 82º apparent field. Look up yours, well call this angle θ_a. then perform the calculation:

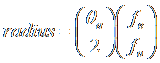
where ,

radius is the angular distance from the center of view to the edge
is the apparent field of view

is the focal length of the telescope

is the focal length of the eyepiece.

Remember this information for later, as it will help you in the future for tasks such as star hopping.

6. Determine the direction of Alkaid, as seen in the eyepiece. This is the last star in the Big Dipper’s handle. If you don’t have a good view of the Big Dipper, due to the time of year or the time of night, look it up on your planisphere. Assuming your eyepiece is pointing up toward the celestial equator and the meridian, you need to flip the left/right direction as Alkaid is seen with the naked eye, if your scope is a Cassegrain with a diagonal or refractor with a diagonal. Look into the eyepiece with the tip of your head pointing true North. If your setup is a Cassegrain or refractor on axis (no diagonal), or a Newtonian telescope, the direction to Alkaid in the eyepiece is the exact opposite of the naked eye direction (seen notes below).

7. Next we need to make another calculation, which is the amount of adjustment we need to do, in units of this radius. So we simply divide 0.7º by this radius, in units of degrees:

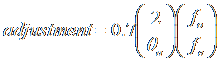
which has units of the radius. For low power setups, or for eyepieces with a very large apparent field of view, the adjustment might be less than 1. For higher power setups, the adjustment might be greater than 1 – meaning that you will need to make the adjustment from the center to the edge of the eyepiece, then a little bit more.

Don’t be afraid of some simple math. You only need to make the calculation once for a given telescope eyepiece combination. You can do it ahead of time. As a matter of fact, go ahead and do it right now. Write down the results and you won’t need to do it again in the field.

8. Now make the adjustment. The naked eye direction to Alkaid shown in the figure below is just an example. You will need to determine this direction yourself as described in step 6.

The above figure shows and example using a Cassegrain or refractor setup, with a diagonal.

Special note to users viewing with a Newtonian reflector, or for Cassegrain or refractor telescopes on-axis, without a diagonal:

In this configuration you need to flip both the left/right and up/down directions when making the adjustment. Simply speaking, the direction to Alkaid as seen in the eyepiece is the exact opposite of its naked eye direction. All else is the same in the above procedure.

Special note to Newtonian reflector telescope users:

The procedure described in this section (after flipping the up/down direction as well as the left/right direction, as described in the above paragraph) works verbatim with a Newtonian reflector telescope design, but only if the OTA is rotated such that the eyepiece is pointed up and the tip of your head is pointed toward true North when making the adjustment. But this may not be the most comfortable position, if even practical. Generally speaking, my best advise in determining the direction to Alkaid in your eyepiece, with an arbitrary OTA rotation and head position, is to make slight altitude and azimuth adjustments and take note of how they affect the view in the eyepiece. They will always be in the form of the figure below where Up-Down correspond to altitude adjustments and Right-Left correspond to azimuth adjustments,

Example eyepiece view using a Newtonian telescope design

except the rotation may be different. All the equations discussed above are still valid, it’s just a matter of figuring out the direction to Alkaid, for your given eyepiece and head position. You’re smart. You can figure it out.

9. If your scope has an electronic GoTo system, you now need to proceed alignment process for that. This process involves slewing to one or more stars, and centering them in your eyepiece. As part of that alignment, your GoTo system may slew to a star and instruct you to make altitude and azimuth adjustments to center the star (for example, the Meade Autostar II system slews to where it thinks Polaris is, and instructs you to center it using the mount’s altitude and azimuth controls). Do not adjust the altitude and azimuth controls, even though your GoTo system, instructs you to do so! Instead, use your GoTo system’s handbox controller to center the star. By properly following steps 1 through 8, you have already polar aligned your mount better than what your GoTo system is capable of doing. After step 8, do not touch the altitude and azimuth controls again, excepting for precise polar alignment described in the next section. You will still need to center a star or two for your GoTo system alignment, but do so using the RA and declination adjustments on the handbox controller. And yes, it’s worth repeating, properly following the above procedure is more accurate than what an electronic GoTo system is capable of, in terms of polar alignment.

Southern hemisphere:

The above procedure generally applies to the southern hemisphere, except you don’t have the luxury of using a nice, bright pole star. We at the Shady Crypt are not as experienced with southern hemisphere alignment, but I might suggest using the northern hemisphere procedure, except start with Sigma Octantis (rather than Polaris), and make your adjustment about 1º toward Delta Chamaeleontis. But you may find it more comfortable using your own set of stars that are readily visible given your particular light pollution situation. You’re smart. You can figure it out. In any case, you can always perform this step roughly, or even skip it altogether, compensating for any inaccuracy by performing a quick iteration of the precise polar alignment procedure described in the next section.

The Collins method of precise polar alignment

About the only reason to do precise polar alignment is for astrophotograhy, or for practicing your skill of the art. If you are just setting up for a night of visual observing, stop here and get to the observing. Seriously, We’ve used the better polar alignment method described above and had no appreciable drift for a half an hour in a high-power eyepiece (although some nights are better than others, they all have very little drift). It’s really that good. Continue on with the Collins method of precise polar alignment only if you need really, really precise alignment.

The Collins method of precise polar alignment is based on the well established drift method of precise polar alignment, except it doesn’t heavily rely on iterative steps – meaning it’s just as precise, and much faster. Tired of spending 90+ minutes trying to perform precise polar alignment, and still seeing drift? Then the Collins method of precise polar alignment is for you. At your next star party, you’ll have already taken multiple astrophoto exposures while your friends are still struggling with their drift-adjust-repeat, drift-adjust-repeat, drift-adjust-repeat, again and again and again methods. The Collins method requires a couple of calculations, but each calculation can be done while you are waiting for the single interval of drift (per azimuth or altitude adjustment), or can even be done beforehand. There’s no time lost by working the calculations. In the end, you’ll be glad you wrote down these equations. You shall bask in the starry heavens and cackle at your stymied, mathematically challenged company while they endlessly wallow in their reticle monotony.

The Collins method of precise polar alignment was developed by Mark Collins, of the Shady Crypt Observatory, in 2008. At the time of this writing, the procedure seems unique. If in the future, it is determined that this method is credited elsewhere by a previous work, Collins will be removed from the procedure’s name. For exact solutions and derivations, see the Collins method of precise polar alignment derivation page.

You will need a reticle eyepiece for this procedure.

Moderate Latitudes:

Start by performing the better alignment procedure discussed above. Then perform the azimuth alignment discussed in this section before moving on to the altitude alignment. The order is important. Perform precise azimuth alignment first, precise altitude alignment second.

Azimuth alignment:

1. Find a star near the intersection of the celestial equator and meridian, and direct your telescope to it (via the right ascension and declination).

2. Vary the right ascension slightly while looking through the eyepiece. Twist the eyepiece until the right ascension adjustment motion is parallel with one set of crosshairs.

3. Center the star in the eyepiece, and take note of the time. You will now allow the star to drift North or South. If you don’t have a motorized mount, track the star using the right ascension only. You only need to be concerned with the North-South drift.

4. If you haven’t done so already, calculate the coefficient of azimuth adjustment, C_az.

where L is your latitude. You can calculate this beforehand, or you can calculate it while your star is drifting.

5. Eventually, you will need to stop waiting and make an azimuth adjustment. You should let the star drift long enough such that the mount’s periodic errors (via mechanical imperfections in the worm gears, etc.) are not a major factor, but not so much that the star drifts out of the field of view. 5 to 20 minutes is usually reasonable. Take note of the time difference between this step and step 3. This is denoted as the drift time, t, in units of minutes.

6. Make your azimuth adjustment. The adjustment causes the star to move East and West in the eyepiece. Make the adjustment so it moves the star in the correct direction, shown in the figures below, for your particular setup and location. The amount of adjustment is given by:

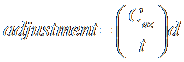where t is the drift time in minutes, and d is the magnitude of the drift (as seen in the eyepiece).

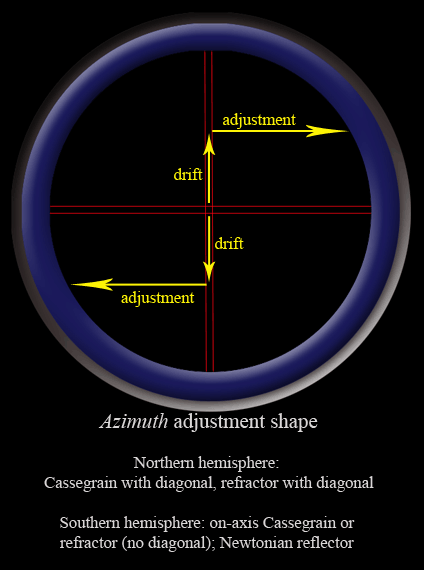
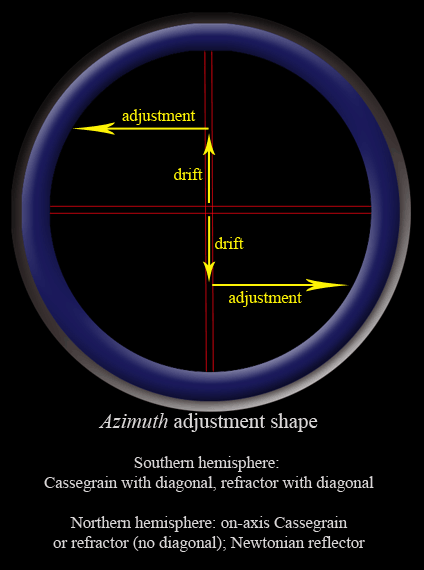
7. That’s it! Now you can move on to the altitude adjustment. This is where the Collins method of precise polar alignment differs from the more conventional drift method. If you were instead using the conventional drift method, this step would be “repeat all of the above again and again and again, until you don’t see any more drift.” By using the Collins method of precise polar alignment, you have just performed all the azimuth adjustment you need, in one fell swoop. Of course you could perform another iteration for extreme accuracy if you wanted to, but I think you’ll find that it’s normally unnecessary.

For exact solutions and derivations, see the Collins method of precise polar alignment derivation page.

Altitude alignment:

1. Pick a star, also on the celestial equator, but either in the East or West, about 20º or maybe a little more above the horizon. The reason it needs to be a minimum angular distance above the horizon is to reduce atmospheric refraction.

2. Direct your telescope to this star (via right ascension and declination), and center the star in your reticle eyepiece.

3. Estimate this star’s right ascension, relative to the horizon, in units of degrees (right ascension is traditionally measured in hours, arcminutes, and arcseconds; but for our purposes, measuring it in units of degrees is more convenient). We are concerned with the absolute value here, so even if the star is in the West, the value is a positive number. A good method for this estimation can be done using your hand. Spread your fingers and thumb apart as far as they will go. Stretch your arm out in front of you, keeping both your shoulders square, at right angles to the direction in front of you. The angular distance from the tip of your pinky finger to the tip of your thumb is about 20º. Now make a fist. The distance from the top to the bottom of the fist is about 10º. Remember, you are estimating the star’s relative right ascension not altitude, so when making your estimate, your hand is tilted from straight up and down by the amount of your latitude. We denote the star’s relative right ascension above the horizon as , in units of degrees.

4. Take note of the time (recentering the star if necessary). You are now going to let the star drift. Like before, you are only concerned with the North-South drift.

5. If you haven’t done so already, calculate the coefficient of altitude adjustment, C_alt.

where is the star’s relative right ascension above the horizon (relative to the eastern horizon if the star is in the East, and relative to the western horizon if the star is in the West – always a positive number), in units of degrees, at the start time of the drift.

6. Eventually, you will need to stop waiting and make an altitude adjustment. You should let the star drift long enough such that the mount’s periodic errors (via mechanical imperfections in the worm gears, etc.) are not a major factor, but not so much that the star drifts out of the field of view. In the case of the star being in the West, you’ll also want to make sure that the star doesn’t drift below about 20º altitude. 5 to 20 minutes is usually reasonable. Take note of the time difference between this step and step 4. This is denoted as the drift time, t, in units of minutes.

7. Make the altitude adjustment. The adjustment will move the star in the North-South axis, just like the drift. Make the adjustment so that the star moves in the opposite direction of the drift, if the star is in the East, and the same direction as the drift, if the star is in the West. The amount of adjustment is determined by

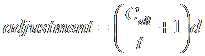, if the star is in the East, or

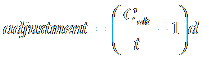, if the star is in the West,

where t has units of minutes and d is the magnitude of drift (as seen in the eyepiece).

That’s it! You’re finished. This is where the Collins method of precise polar alignment differs from the more conventional drift method. If you were instead using the conventional drift method, this step would be “repeat all of the above again and again and again, until you don’t see any more drift.” By using the Collins method of precise polar alignment, you have just performed all the altitude adjustment you need, in one fell swoop. Of course you could perform another iteration for extreme accuracy if you wanted to, but I think you’ll find that it’s normally unnecessary.

You may be wondering why the equations are different for East and West, and where the ±1 comes from. It comes from the fact that you estimate the star’s right ascension before you allow the star to drift, and you make the adjustment after the drift. In the case of the star in the East, it will rise to a region of the sky where the star’s apparent motion in the field of view is more sensitive to altitude adjustments. In the case of the West, the star moves into a region where its apparent motion is less sensitive to altitude adjustment.

If you’re mathematically acute, may have already noticed that in the case of the star in the West, things seem odd if you let the star drift long enough such that . In that case, the adjustment = 0, even though there might be drift. “How can that be?” The reason is because if you let the star drift for the time it takes for, it is approximately the amount of time it takes for that star to reach the horizon! When the star is at the horizon, altitude adjustments have no effect on the star’s apparent motion in the eyepiece (it only rotates the field of view). Of course, this is not a realistic situation since you would never let the star drift for that long. You can always assume that C_alt/t will be greater than 1 for practical reasons.

For exact solutions and derivations, see the Collins method of precise polar alignment derivation page.

Tropical latitudes:

In deep, tropical latitudes, you don’t have the luxury of picking a star at the celestial equator and meridian intersection for making azimuth adjustments. When at the equator, making an azimuth adjustment merely rotates the field of view for a star at the celestial equator meridian intersection (which in this special case, happens to be at the zenith). Obviously, a star in a different location is necessary.

Azimuth alignment:

1. Pick a star near the meridian, and about 20º or so down from the celestial equator. If you’re in the northern hemisphere, pick a star south of the celestial equator. If you’re in the southern hemisphere, pick a star north of the celestial equator. Estimate the magnitude of the star’s declination. A good method for this can be done using your hand. Spread your fingers and thumb apart as far as they will go. Stretch your arm out in front of you, keeping both your shoulders square, at right angles to the direction in front of you. The angular distance from the tip of your pinky finger to the tip of your thumb is about 20º. Now make a fist. The distance from the top to the bottom of the fist is about 10º. You are interested in the (absolute value) of the star’s declination relative to the celestial equator. We denote the star’s declination magnitude as , in units of degrees.

2. Calculate the coefficient of azimuth adjustment, C_az.

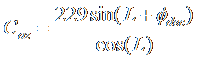
where L is your latitude, and is the absolute value of the star’s declination.

3. Follow the Collins method of precise polar alignment azimuth alignment for moderate latitudes procedure, except use the new equation and corresponding value for C_az.

Altitude alignment:

Follow the Collins method of precise polar alignment altitude alignment for moderate latitudes procedure. No modifications are necessary.

Arctic and Antarctic latitudes:

Extremely high latitudes introduce a number of problems. The major one is not being able to choose a star on the celestial equator for azimuth or altitude alignment. This is because no stars on the celestial equator make it very far above the horizon; and near the horizon, atmospheric refraction is an issue. We’ll obviously need to pick different locations for both. Time to bundle up good, and break out the akvavit (we recommend Linie aquavit, given each bottle’s long travels, it seems a particularly appropriate brand for polar alignment). Using the method described below, you may start with either the azimuth or altitude alignment first. The order is not so important in this case. Because the drift due to azimuth error is much smaller at high latitudes, it actually may make more sense to start with altitude alignment.

Azimuth alignment:

1. Pick a star near the meridian, and about 10-20º or so up from the celestial equator. If you’re in the northern hemisphere, pick a star north of the celestial equator. If you’re in the southern hemisphere, pick a star south of the celestial equator. Estimate the magnitude (absolute value) of the star’s declination magnitude. A good method for this can be done using your hand. Spread your fingers and thumb apart as far as they will go. Stretch your arm out in front of you, keeping both your shoulders square, at right angles to the direction in front of you. The angular distance from the tip of your pinky finger to the tip of your thumb is about 20º. Now make a fist. The distance from the top to the bottom of the fist is about 10º. You are interested in the absolute value of the star’s declination relative to the celestial equator. We denote the star’s declination magnitude as , in units of degrees.

2. Calculate the coefficient of azimuth adjustment, C_az.

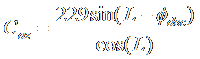
where L is your latitude, and is the absolute value of the star’s declination.

3. Follow the Collins method of precise polar alignment azimuth alignment for moderate latitudes procedure, except use the new equation and corresponding value for C_az.

Altitude alignment:

1. In arctic and Antarctic latitudes, the altitude alignment makes a dramatic turnaround compared to the procedure for moderate latitudes. Instead of picking a star near the east or west on the celestial equator, pick a star 90º from the celestial equator, relative to directly East or West, that is at least about 20º or so above the horizon. In other words, pick a star on an imaginary line that intersects directly East or West, and the celestial pole (the celestial pole won’t be too far from straight up at these latitudes).

Picking a star on the celestial equator has the advantage of maximizing the rate of drift across the sky – but in arctic and Antarctic latitudes, you don’t have the luxury of picking a star on the celestial equator, due to atmospheric refraction. So instead, pick a star along the line that intersects either East or West, and the celestial pole. This imaginary line is perpendicular to the celestial equator, and has the desirable property of minimizing the effects of residual azimuth alignment errors, as long as the azimuth alignment is even roughly close to being okay. So even if you’ve drank too much akvavit while performing the azimuth alignment procedure discussed above, it shouldn’t have a major impact on your altitude alignment (hypothermia is a different story, however – but we at the Shady Crypt are an odd sort).

2. Estimate the magnitude of the star’s declination magnitude. A good method for this can be done using your hand. Spread your fingers and thumb apart as far as they will go. Stretch your arm out in front of you, keeping both your shoulders square, at right angles to the direction in front of you. The angular distance from the tip of your pinky finger to the tip of your thumb is about 20º. Now make a fist. The distance from the top to the bottom of the fist is about 10º. You are interested in the absolute value of the star’s declination relative to the celestial equator. We denote the star’s declination magnitude as , in units of degrees. (note that this is a different star, and thus a different , than was used in the azimuth alignment procedure [just a friendly reminder in case the aquavit is really kicking in]).

3. Take note of the time (recentering the star if necessary). You are now going to let the star drift. Like before, you are only concerned with the North-South drift.

4. If you haven’t done so already, calculate the coefficients of altitude adjustment, C_altEW and C_altNS.

where is the absolute value of the star’s declination, in units of degrees. You actually only need one of the coefficients, but it’s easy enough to calculate both.

6. Make the altitude adjustment. The adjustment will move the star in both the East-West axis and the North-South axis. The amount of adjustment in each axis is determined by

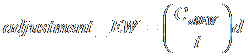
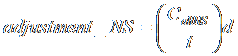
where t has units of minutes and d is the magnitude of drift (as seen in the eyepiece). Note that you are only making one adjustment. There are two coefficients, only because your single adjustment moves the star in both the East-West and North-South directions. Use the figures below to determine the direction of adjustment, based on your setup and location. Note that for any particular setup, the East-West direction the star moves in the altitude adjustment is the opposite direction of movement in the azimuth adjustment.

The procedure and shape is the same whether the star in the East or the West. Only your setup and latitude (i.e. near the North pole or near the South pole) affect the shape.

7. That’s it! You’re finished. This is where the Collins method of precise polar alignment differs from the more conventional drift method. If you were instead using the conventional drift method, this step would be “repeat all of the above again and again and again, until you don’t see any more drift.” By using the Collins method of precise polar alignment, you have just performed all the altitude adjustment you need, in one fell swoop. Of course you could perform another iteration for extreme accuracy if you wanted to, but I think you’ll find that it’s normally unnecessary.

For exact solutions and derivations, see the Collins method of precise polar alignment derivation page.

Home