Collins method of polar alignment derivation
The
math behind the magic
If you havenít done so already, first see the page that describes the actual method. You can click here to view the page.
This page derives the equations used in the Collins Method of Precise Polar Alignment.†
Introduction to polar alignment mathematics
The mathematics used to derive the Collins method of precise polar alignment are relatively simple. Just a few geometry principles and a little trigonometry are the only things involved.
Radians and degrees
Angles can be expressed in units of
radians or degrees. We will use both our equations, but in general, radians are
used more often, and may later be converted to degrees in our final solutions.
When actually performing polar alignment in the field, degrees are more
convenient to work with. But for the purposes of our derivations, keeping
angles in units of radians allows us to take advantage of certain geometrical
and trigonomic principles. For example, when
calculating the length of an arc on a circle in two dimensional plane geometry,
the length of the arc is the angle swept out by the arc,![]() , multiplied by the radius of the
circle (or the distance of the arc from the point of convergence of the two
lines).
, multiplied by the radius of the
circle (or the distance of the arc from the point of convergence of the two
lines).
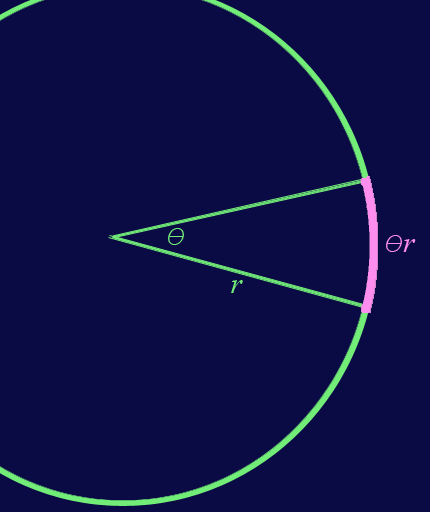
But this is true only if![]() is expressed in radians. The result,
is expressed in radians. The result,![]() , has units of whatever units
, has units of whatever units ![]() has. For example, if
has. For example, if ![]() has units of meters, then the arc length,
has units of meters, then the arc length, ![]() , also has units of meters, and not radian times meters.
, also has units of meters, and not radian times meters.
Trigonomic
functions such as sin() and cos()
can operate in degrees or radians, as long as consistency is maintained within
the brackets. For example, if a given angle is expressed in ![]() †radians or
†radians or ![]() †degrees, then
†degrees, then
![]() ,
,
where the
first sin() function operates in radians and the second sin() function operates
in degrees. Itís the same angle. So the sine of the same angle gives the same
value. But certain identities and approximations can only take place if the
angle is represented in radians. For example, if the angle ![]() †is less than around
†is less than around ![]() †(less then around
10ļ),
†(less then around
10ļ),
![]() ,
,
but only
if ![]() †is expressed in
radians.
†is expressed in
radians.
Angles, angles and more angles
Although the polar alignment mathematics are relatively simple, they are less than straightforward because nearly every parameter we work with is an angle. Letís go back to our plane geometry arc length example. In polar alignment mathematics, it would be more typical that the radius of the circle is actually an angle itself in some form or another.
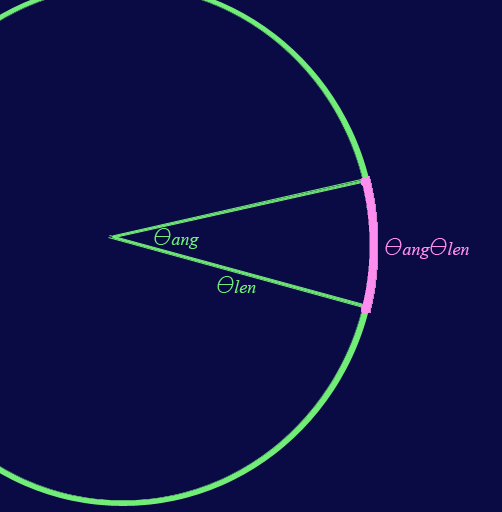
Here, ![]() †represents the radius
of the circle, but also has units of radians most likely because it is an angle
itself somewhere in the bigger picture.
†represents the radius
of the circle, but also has units of radians most likely because it is an angle
itself somewhere in the bigger picture. ![]() †operates
here as a true angle. The resulting
arc length,
†operates
here as a true angle. The resulting
arc length, ![]() , has units of radians (not rad2), and is
itself an angle of sorts.
, has units of radians (not rad2), and is
itself an angle of sorts.
Spheres
The reason why so many angles is because we are working in 3 dimensions. On star charts, celestial maps, and of course in polar alignment, the sky is represented by a sphere of radius 1. Distance, such as the angular distance between two stars (from our perspective), is the arc length from one star to another on this sphere. The arc length is used as a form of distance, but in fact it is technically an angle.
Measuring the arc length on the surface of a radius 1 sphere is a little different than on a 2 dimensional circle.
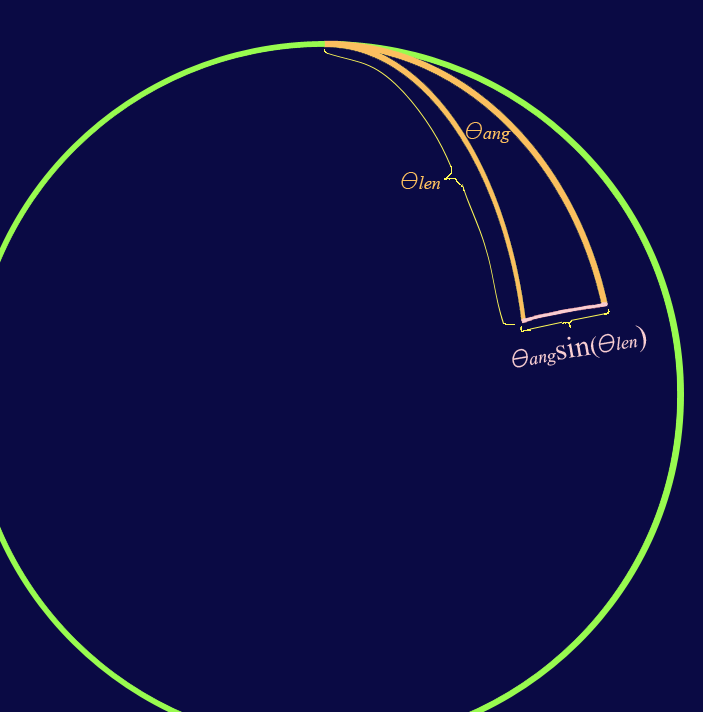
Lines initially diverge from each
other at the ![]() †angle
, but as the lengths of these lines reach
†angle
, but as the lengths of these lines reach ![]() , they have become parallel (at which point the distance
between the lines on the sphereís surface is exactly
, they have become parallel (at which point the distance
between the lines on the sphereís surface is exactly ![]() ). If these lines continue to increase in length, they will
converge again as they reach the length
). If these lines continue to increase in length, they will
converge again as they reach the length ![]() . So on the surface of a radius 1
sphere, arc lengths are calculated by the angle swept out by the arc,
multiplied by the sine of the
distance from the point of convergence.
. So on the surface of a radius 1
sphere, arc lengths are calculated by the angle swept out by the arc,
multiplied by the sine of the
distance from the point of convergence.
Notice that if ![]() †is small, the arc length approaches that of
the 2 dimensional plane geometry solution. This is because if
†is small, the arc length approaches that of
the 2 dimensional plane geometry solution. This is because if ![]() †is small,
†is small, ![]() . Thus the arc length reduces to
. Thus the arc length reduces to ![]() †for small
†for small
![]() .
.
Trigonometry
If you understand the above principles, then you have about everything you need to understand the derivations below. The only other thing is a small group of trigonomic identities and approximations that we will take advantage of, on occasion.
Identities:
![]()
![]()
![]()
Standard approximations (used only where explicitly indicated in the text):
![]() ,
for small
,
for small ![]() .
.
![]() , for
small
, for
small ![]() .
.
![]() ,
for small
,
for small ![]() .
.
Azimuth alignment derivations
Assumptions
It is assumed that altitude alignment is good. In practice, a star is picked near the meridian, where altitude alignment error is minimized. As a matter of fact, if the star is actually on the meridian, the effect of altitude error on the starís apparent declination drift is zero. However if the star is not exactly on the meridian, the declination drift due to altitude error begins to increase as the star approaches the horizon. This effect on declination drift due to residual altitude error is not taken into account using these equations. This is the very reason why we pick a star near the meridian: because stars on the meridian have a negligible declination drift due to residual altitude error.
Approximations
We approximate that on the
celestial equator, a starís apparent rate of drift across the sky is ![]() †radians/minute. Itís
actually ever so slightly more than that. But for our purposes, the approximate
rate of motion of
†radians/minute. Itís
actually ever so slightly more than that. But for our purposes, the approximate
rate of motion of ![]() †rad/min is
good enough.
†rad/min is
good enough.
We apply the standard approximations listed in the previous section, where explicitly stated in the text, before finalizing the equations.
Moderate latitudes
Definition of variables:
![]() :†††††††† Time, in units of minutes
:†††††††† Time, in units of minutes
R:†††††††† Rate of drift across the sky for a star on the celestial equator. Approximately π/720 rad/min.
![]() :†††† Azimuth
error, in units of radians.
:†††† Azimuth
error, in units of radians.
L:†††††††† absolute value of the latitude of the observing location (can be left in units of degrees).
d:†††††††† Magnitude of the starís declination drift (i.e North-South drift), in units of radians.
aaz:†††††† Magnitude of the apparent motion of the star in the eyepiece, as a result of azimuth adjustments.

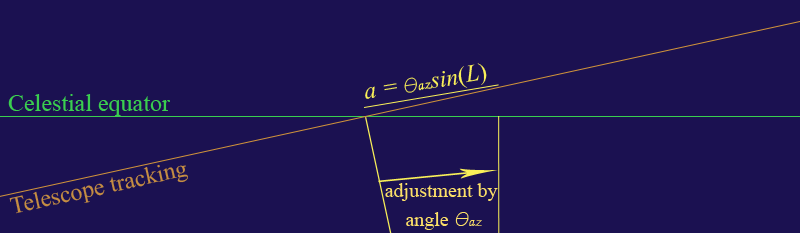
There are two lines on the radius 1
sphere that concern us. The first is the celestial equator itself, and the
second is line nearly parallel to the celestial equator, but skewed by a slight
angle ![]() .
The latter is the line that the telescope tracks. The cos(L)
term comes from the fact that the drift due to azimuth error becomes smaller at
higher latitudes. Hypothetically, if you were precisely at the North or South pole, the celestial pole would be directly above, and there
would be no drift due to azimuth error at all. The azimuth could be 180ļ wrong, but there would still be
no declination drift! Of course, weíre working with moderate latitudes here,
but you get the idea.
.
The latter is the line that the telescope tracks. The cos(L)
term comes from the fact that the drift due to azimuth error becomes smaller at
higher latitudes. Hypothetically, if you were precisely at the North or South pole, the celestial pole would be directly above, and there
would be no drift due to azimuth error at all. The azimuth could be 180ļ wrong, but there would still be
no declination drift! Of course, weíre working with moderate latitudes here,
but you get the idea.
Using the principles discussed in the previous section, a starís declination drift at the intersection of the celestial equator and the meridian is
![]() .
.
When we make our adjustment, we
must adjust the azimuth by
![]() . The apparent motion of the star in the eyepiece, is
. The apparent motion of the star in the eyepiece, is
![]() .
.
When Rt reaches ![]() †(meaning
the star has drifted to the horizon), the apparent motion is equal to
†(meaning
the star has drifted to the horizon), the apparent motion is equal to ![]() , which makes sense, since any star on the horizon will
have an apparent motion of
, which makes sense, since any star on the horizon will
have an apparent motion of ![]() †when an adjustment of
†when an adjustment of ![]() †is made. Also notice that the equation
reduces to
†is made. Also notice that the equation
reduces to
![]() ,†
for small t,
,†
for small t,
as shown in the figure below.†
Combining the drift and adjustment equations, we obtain
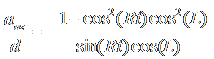 .
.
Applying our standard approximations, and utilizing one our trigonomic identities, the equation reduces to
![]() ,†††
for small t.
,†††
for small t.
Given that ![]() , our final equation is
, our final equation is
![]() .
.
The approximation holds pretty well for t up to around 40 minutes.
Tropical latitudes
Definition of variables:
t:††††††††† Time, in units of minutes
R:†††††††† Rate of
drift across the sky for a star on the celestial equator. Approximately
![]() †rad/min.
†rad/min.
![]() :†††† Azimuth error, in units of radians.
:†††† Azimuth error, in units of radians.
L:†††††††† Absolute value of the latitude of the observing location in units of degrees.
![]() :††† Absolute value of the starís
declination, in units of degrees.
:††† Absolute value of the starís
declination, in units of degrees.
d:†††††††† Magnitude of the starís declination drift (i.e North-South drift), in units of radians.
aaz:†††††† Magnitude of the apparent motion of the star in the eyepiece, as a result of azimuth adjustments.
There are two lines on the radius 1
sphere that concern us. The first is the line of constant declination† itself, and the second is line nearly
parallel to the first, but skewed by a slight angle ![]() †. The latter is
the line that the telescope tracks. Using the principles discussed in the
previous section, a starís declination drift at the intersection of the given
declination and the meridian is
†. The latter is
the line that the telescope tracks. Using the principles discussed in the
previous section, a starís declination drift at the intersection of the given
declination and the meridian is
![]() .
.
When we make our adjustment, we
must adjust the azimuth by ![]() .
The apparent motion of the star in the eyepiece, is
.
The apparent motion of the star in the eyepiece, is
![]() .
.
Notice that the equation reduces to
![]() ,†
for small t,
,†
for small t,
as shown in the figure below.†
Combining the drift and adjustment equations, we obtain
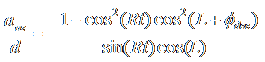 .
.
Applying our standard approximations, and utilizing one our trigonomic identities, the equation reduces to
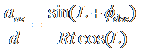 ,†††
for small t.
,†††
for small t.
Given that ![]() , our final equation is
, our final equation is
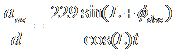 .
.
The approximation holds pretty well for t up to around 40 minutes.
Arctic and Antarctic latitudes
Definition of variables:
t:††††††††† Time, in units of minutes
R:†††††††† Rate
of drift across the sky for a star on the celestial equator. Approximately
![]() †rad/min.
†rad/min.
![]() :†††† Azimuth
error, in units of radians.
:†††† Azimuth
error, in units of radians.
L:†††††††† Absolute value of the latitude of the observing location in units of degrees.
![]() :††† Absolute
value of the starís declination, in units of degrees.
:††† Absolute
value of the starís declination, in units of degrees.
d:†††††††† Magnitude of the starís declination drift (i.e North-South drift), in units of radians.
aaz:†††††† Magnitude of the apparent motion of the star in the eyepiece, as a result of azimuth adjustments.
There are two lines on the radius 1
sphere that concern us. The first is line of constant declination itself, and the
second is line nearly parallel to the first, but skewed by a slight angle ![]() †. The latter is
the line that the telescope tracks. The cos(L)
term comes from the fact that the drift due to azimuth error becomes smaller at
higher latitudes. Hypothetically, if you were precisely at the North or South
pole, the celestial pole would be directly above, and there would be no drift
due to azimuth error at all. The azimuth could be 180ļ wrong, but there would still be no declination
drift!
†. The latter is
the line that the telescope tracks. The cos(L)
term comes from the fact that the drift due to azimuth error becomes smaller at
higher latitudes. Hypothetically, if you were precisely at the North or South
pole, the celestial pole would be directly above, and there would be no drift
due to azimuth error at all. The azimuth could be 180ļ wrong, but there would still be no declination
drift!
Using the principles discussed in the previous section, a starís declination drift at the intersection of the given declination and the meridian is
![]() .
.
When we make our adjustment, we
must adjust the azimuth by ![]() . The apparent motion of the star in the eyepiece, is
. The apparent motion of the star in the eyepiece, is
![]() .
.
Combining the drift and adjustment equations, we obtain
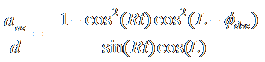 .
.
Applying our standard approximations, and utilizing one our trigonomic identities, the equation reduces to
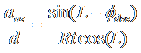 ,†††
for small t.
,†††
for small t.
Given that ![]() , our final equation is
, our final equation is
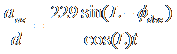 .
.
The approximation holds pretty well for t up to around 40 minutes.
Altitude alignment derivations
Assumptions
It is assumed that azimuth alignment is good. The effect on declination drift due to residual altitude error is not taken into account using these equations. In general, azimuth alignment should be done prior to altitude alignment. An exception to the order can be made in arctic and Antarctic latitudes, where either may be performed first.
Approximations
We approximate that on the
celestial equator, a starís apparent rate of drift across the sky is ![]() †radians/minute. Itís
actually ever so slightly more than that. But for our purposes, the approximate
rate of motion of
†radians/minute. Itís
actually ever so slightly more than that. But for our purposes, the approximate
rate of motion of ![]() †rad/min
is more than good enough.
†rad/min
is more than good enough.
We apply the standard approximations listed in a previous section, where explicitly stated in the text, before finalizing the equations.
Moderate and tropical latitudes
Definition of variables:
t:††††††††† Time, in units of minutes
R:†††††††† Rate
of drift across the sky for a star on the celestial equator. Approximately
![]() †rad/min.
†rad/min.
![]() :†††† Altitude error, in units of radians.
:†††† Altitude error, in units of radians.
![]() :†††† Absolute
value of right ascension, relative to nearest horizon, in units of radians.
Must be measured at the start time of the drift.
:†††† Absolute
value of right ascension, relative to nearest horizon, in units of radians.
Must be measured at the start time of the drift.
![]() :††††† Same thing
as
:††††† Same thing
as ![]() except in units of degrees.
except in units of degrees.
d:†††††††† Magnitude of the starís declination drift (i.e North-South drift), in units of radians.
aalt:†††††† Magnitude of the apparent motion of the star in the eyepiece, as a result of altitude adjustments.
Star near the eastern horizon
If you start with a star on the
celestial equator, near the eastern horizon, the total drift due to altitude alignment
error becomes maximum when the star reaches the meridian. The star reaches the
meridian when ![]() . After that, the star begins to drift back in the other
direction. The equation which describes this is
. After that, the star begins to drift back in the other
direction. The equation which describes this is
![]()
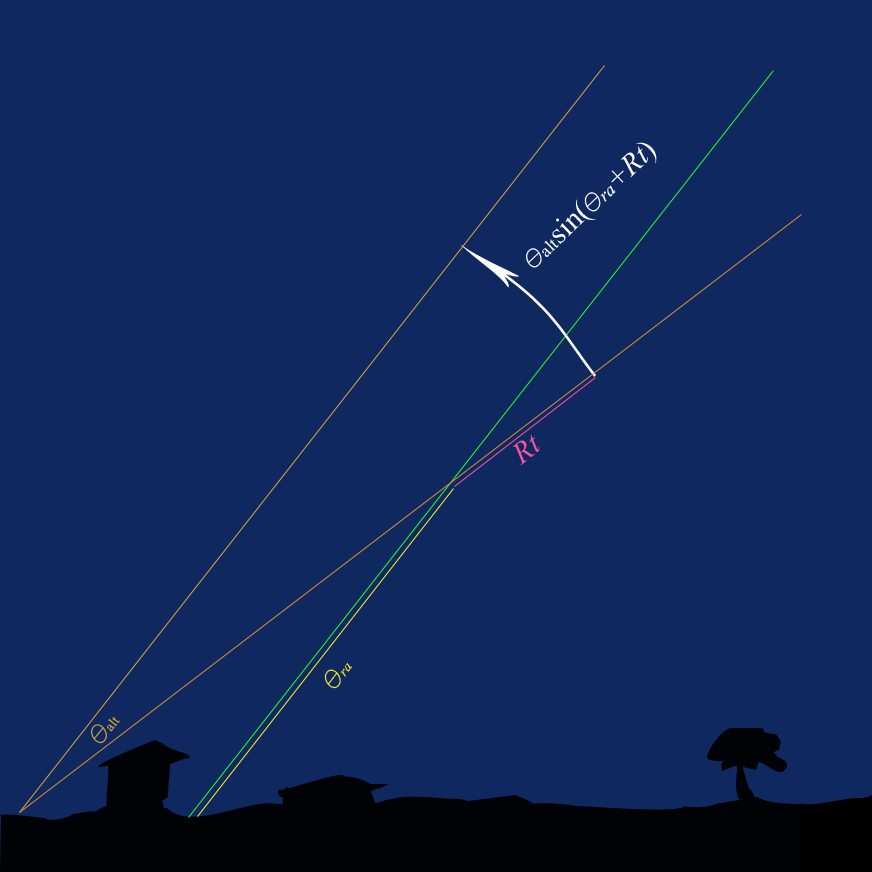
The figure below shows an example eastern horizon in the northern hemisphere.

It is assumed that the altitude
adjustment is ![]() . The apparent movement of the star in the eyepiece
due to adjusting the altitude by
. The apparent movement of the star in the eyepiece
due to adjusting the altitude by ![]() †is
†is
![]() ,
,
as shown in the figure below.
Combining the equations gives us
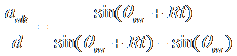 .
.
Using one of our trigonomic identities, this becomes
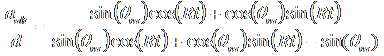 .
.
Applying our standard approximations reduces the equation to
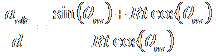 ,††† for small t,
,††† for small t,
and further reduces to
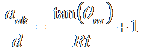 ,†††
for small t.
,†††
for small t.
Given that ![]() ,
our final equation is
,
our final equation is
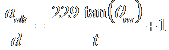 .
.
The approximation holds pretty well for drift times up to around 40 minutes.
Star near the western horizon
For the Western horizon, the math is pretty similar. But it differs in the fact that the star is moving toward the horizon instead of away from it.
Here,
![]()
![]()
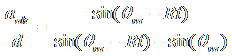 .
.
Using one of our trigonomic identities, this becomes
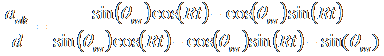 .
.
Applying our standard approximations reduces the equation to
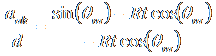 ,††† for small t,
,††† for small t,
and further reduces to
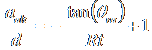 ,†††
for small t.
,†††
for small t.
The negative sign in front of the first term results from the need to make the adjustment in the opposite direction as what is done if the star was near the eastern horizon. But we are not particularly concerned with the direction. We already have that figured out (the adjustment must be done so the star moves in the same direction as the drift, when we use a star near the western horizon). All we need is the magnitude of the adjustment/drift ratio, which is
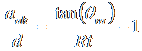
Given that ![]() , our final equation is
, our final equation is
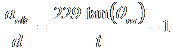 .
.
The approximation holds pretty well for drift times up to around 40 minutes.
Arctic and Antarctic latitudes
Definition of variables:
t:††††††††† Time, in units of minutes
R:†††††††† Rate of drift across the sky for a star on the celestial equator. Approximately π /720 rad/min.
![]() :†††† Altitude
error, in units of radians.
:†††† Altitude
error, in units of radians.
![]() :††† Absolute value of declination, in
units of radians.
:††† Absolute value of declination, in
units of radians.
![]() :††† Same thing as θdec
except in units of degrees.
:††† Same thing as θdec
except in units of degrees.
d:†††††††† Magnitude of the starís declination drift (i.e North-South drift), in units of radians.
aaltEW:†† Magnitude of the apparent motion of the star in the eyepiece, in the East-West direction (right ascesion), as a result of altitude adjustments.
aaltNS:††† Magnitude of the apparent motion of the star in the eyepiece, in the North-South direction (declination), as a result of altitude adjustments.
For high latitudes, we pick a star that lies along the imaginary line between East and the celestial pole, or West and the celestial pole. This line is perpendicular to the celestial equator, and is also perpendicular to the meridian. When a star crosses this line, itís drift due to residual (minor) azimuth adjustment errors are minimized. Itís drift due to altitude alignment error is
![]() .
.
The apparent motion of the star in the eyepiece, in the East-West direction is
![]() .
.
The ![]() term comes from the fact that the overall motion (in any
direction) caused by altitude alignment is zero if
term comes from the fact that the overall motion (in any
direction) caused by altitude alignment is zero if ![]() †is zero, and increases as
†is zero, and increases as ![]() †increases, reaching a
maximum when
†increases, reaching a
maximum when ![]() †is 90ļ. The
†is 90ļ. The ![]() †term comes from fact that as the declination
increases, the apparent motion shifts from the East-West direction to the
North-South direction. With a declination of 90ļ, the apparent motion is
completely in the North-South direction. The cos(Rt) plays a similar role. As the star
reaches the meridian (when
†term comes from fact that as the declination
increases, the apparent motion shifts from the East-West direction to the
North-South direction. With a declination of 90ļ, the apparent motion is
completely in the North-South direction. The cos(Rt) plays a similar role. As the star
reaches the meridian (when ![]() ), the apparent motion of altitude adjustments is completely
in the North-South direction. The apparent motion in the North-South direction
is described by:
), the apparent motion of altitude adjustments is completely
in the North-South direction. The apparent motion in the North-South direction
is described by:
![]() .
.
Combining, we have
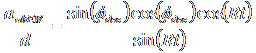
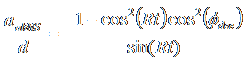 .
.
Applying our standard approximations for small t reduces the equations to
![]() ,†††† for small t,
,†††† for small t,
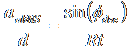 ,††††
for small t.
,††††
for small t.
Given that ![]() , our final equations are
, our final equations are
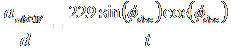 ,
,
![]() .
.
The approximation holds pretty well for drift times up to around 40 minutes.
© Copyright 2008, Mark Collins, Shady Crypt Observatory.